Find a Basis of the Space of Solutions
Linear Algebra 4 | Subspace, Nullspace, Column Space, Row Space, Basis, Dimension, and Rank
![]()

- Subspace
(1) Recall: The Definition of Subspace
Let W be a subset of vector space V ( = ℝⁿ), then W is a subspace of V if provided,
- Condition #1: W is closed under vector addition
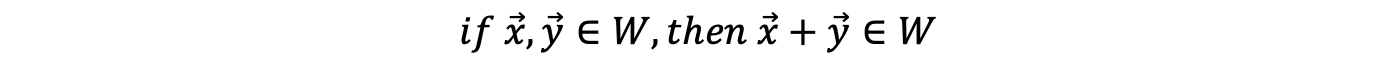
- Condition #2: W is closed under scalar multiplication

- other conditions to be a vector space are inherited by W, for example:
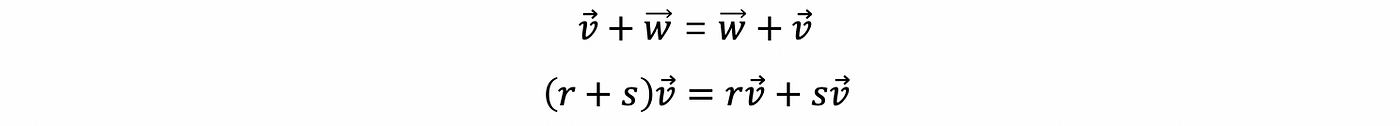
(2) Subspace: Some Examples
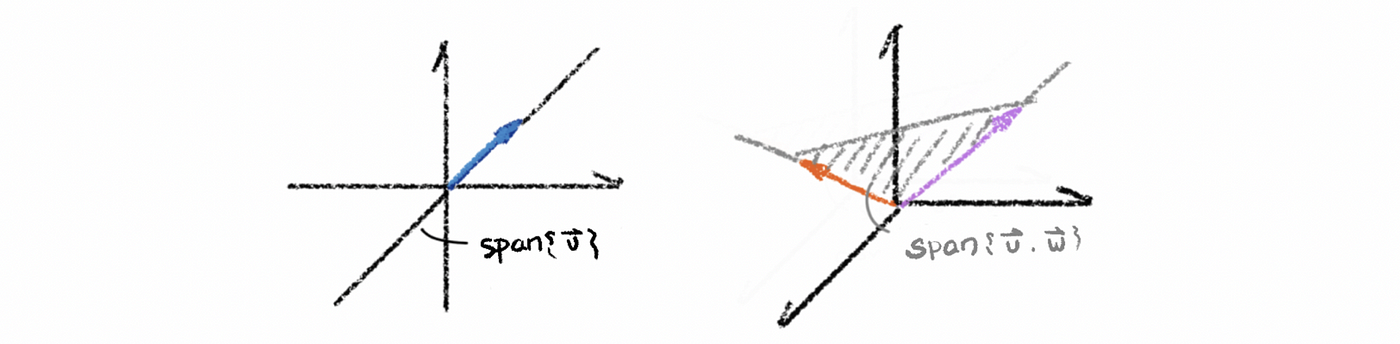
Recall: the span means the set of all vectors in a linear combination of some given vectors
- the span of a set of vectors from V is automatically a subspace of V
- {0} is the trivial subspace
- the span of a single vector v ( ≠ 0 ) in ℝⁿ is a line through the origin
- the span of two non-colinear vectors in ℝⁿ is a plane through the origin in ℝⁿ
(3) Important Note: vector 0 must be in a vector space!
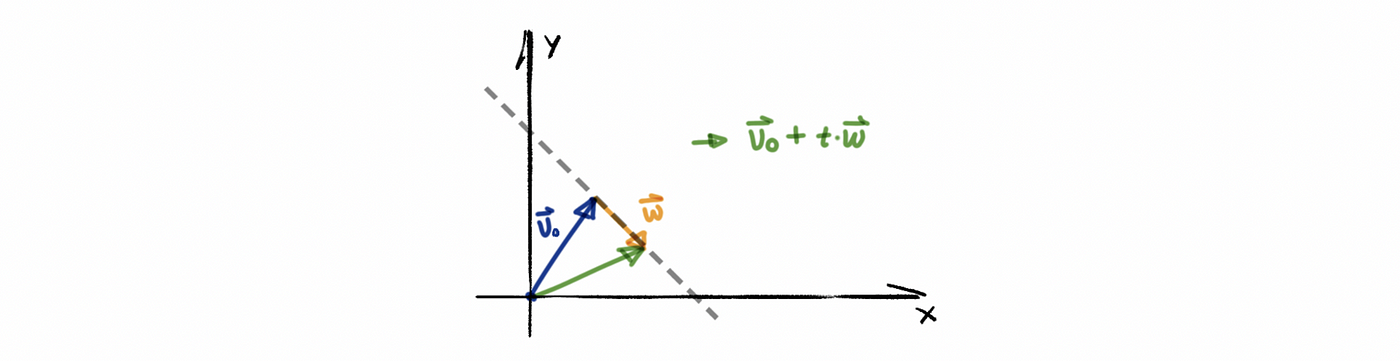
Note that a line not through the origin is NOT a subspace similarly for the plane. (If it does not include the vector 0 and then the subspace is not closed). So that if we want to form a subspace, we can start from the origin, say vector vₒ , and then change its direction by adding vector w in any direction with any length. For example, the following line is not a subspace,
(4) The Definition of Null Space
The set of solutions to the homogenous system Ax = 0 is a subspace of ℝⁿ, where we can also consider it as the span of all the non-trivial solutions, where the size of matrix A is m × n, and A: ℝⁿ → ℝᵐ. If we
- say vector v , w satisfy Av = 0 and Aw = 0 , then check A( v + w )= 0
- say c∈ℝ, and v ∈ℝⁿ with Av = 0 , then A ( c v ) = c · Av = c · 0 = 0
Call this set of solutions to the homogenous system as the null space of matrix A which is notated by N(A). Or we can also call it null(A).

(5) The Definition of Column Space
Another important subspace associated with A of m × n, A: ℝⁿ → ℝᵐ, and

Claim that W is a subspace of ℝᵐ. Reason: W equals the span of the columns of A, because,

We call W the column space of A, and it is notated as col(A) or C(A), which is also the linear combinations of columns of A (aka. image of A, or range of A). Note that the column space is the subspace with all columns of A inside this subspace.
2. Linear Independent
(1) The Definition of Linear Independent
- Perspective #1: only one trivial solution with the linear combination of all these vectors equal zero
A set of vectors { v 1, v 2, …, v k} in a vector space V is linearly independent provided that,
whenever,
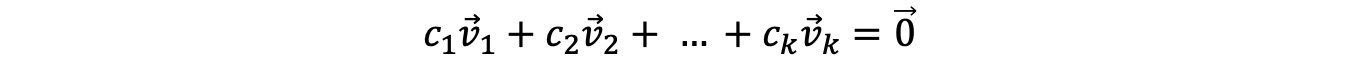
we must have,

So this also means that the only linear combination of these vectors { v 1, v 2, …, v k} that gives 0 is the trivial one.
- Perspective #2: only one trivial solution for the equation system of Ax = 0
Another way to think about linear independent is that if I take { v 1, v 2, …, v k} and put them into a matrix A (as columns) as,
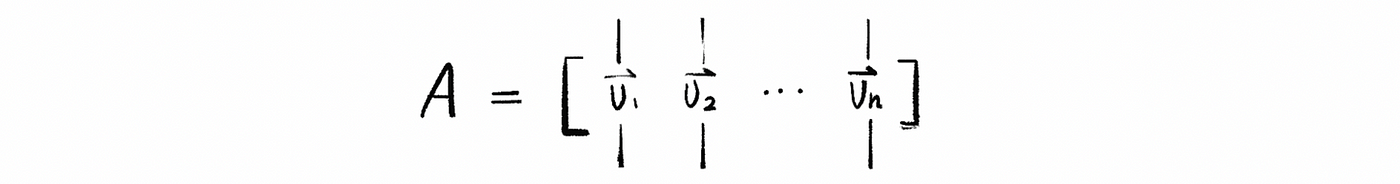
( the size of A is m × k ). Now we have the set {v1, v2, …, vk} is independent ⇔ Ax = 0 has only the trivial solution ( x = 0) ⇔ N(A) = {0}.
To find N(A) for a given matrix A, we can solve the system [ A | 0 ] by row reduction, which is the same as solving the equation of Ax = 0 .
- Perspective #3: one-to-one function view
Another perspective is that because A is m × k, so A: ℝᵏ → ℝᵐ and A is a one-to-one function from ℝᵏ to ℝᵐ. A one-to-one function means that if Av = Aw , then v = w .
Proof:
Note that if Av = Aw ,
then Av -Aw = A( v - w ).
by Perspective #2, we can then have, Ax = 0 ,
so, A( v - w ) = 0
Then v - w = 0
and then we have, v = w .
(2) The Definition of Linearly Dependent
If { v 1, v 2, …, v k} is linearly dependent (not linearly independent), then some linear combination of these variables gives me 0 when the solution is non-trivial. This is also to say that for the equation,

we have not all cis' equal to zero (at least one non-trivial solution).
Proof:
Say if we have a non-trivial solution for the equation with c1 ≠ 0, then we have,
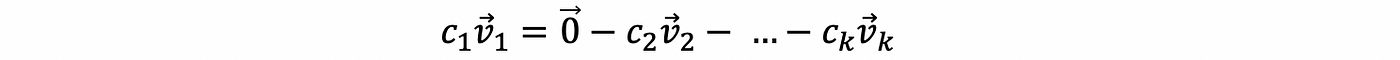
then,
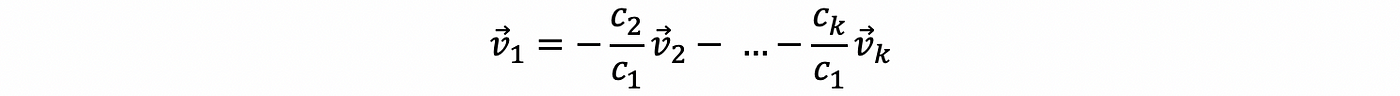
this is to say that the vector v 1 is a linear combination of the other vectors and this means that the vector v 1 is dependent on the other variables.
(3) The Definition of Redundancy
Referring to the previous case of in the previous case of v 1 in the part of linear dependence. As a result, v1 (or some vi) is a linear combination of the other vectors and this is so-called redundancy.
(4) Geometry View of Linear Independence
Suppose we have { v 1, v 2} with v 1, v 2 linearly independent to each other is called non-collinear (not in the same line) geometrically. However, if v 1, v 2 are linearly dependent, these two vectors are collinear (which means that they are in the same line). This is because that for linear dependence, we can have,
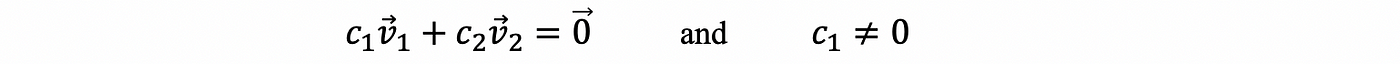
then suppose that,
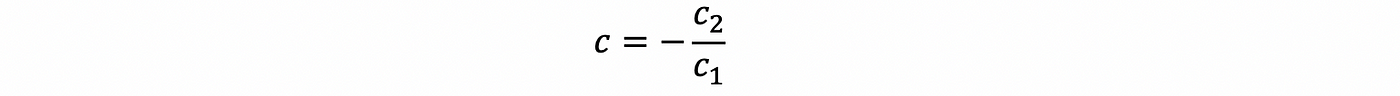
finally, we have,
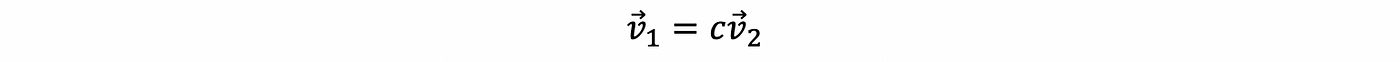

Similarly, { v 1, v 2, v 3} with v 1, v 2, and v 3 are linearly independent and is so-called non-coplanar. However, if v 1, v 2, and v 3 are linearly dependent and is called coplanar.
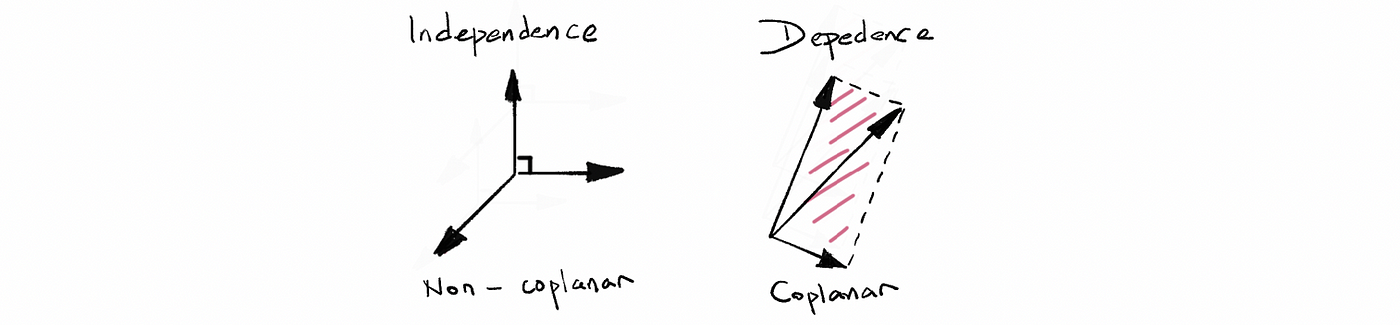
3. Basis and Dimension
(1) The Definition of Basis
Let { v 1, …, v n} be a set of vectors in the vector space V, and if { v 1, …, v n} satisfies,
(a) A spanning set for the vector space V
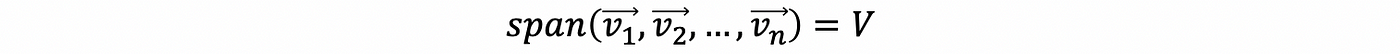
(b) { v 1, …, v n} is linearly independent, recall it as,
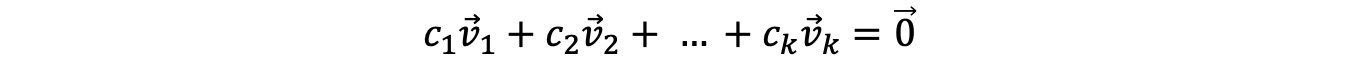
we must have,

Then we call the set { v 1, …, v n} a basis for the vector space V. Note that basis is the smallest (minimized) possible spanning set (without redundancy) or the largest (maximized) possible linearly independent set (because spanning) in the vector space V.
(2) The Definition of Dimension
The dimension of a vector space V is the number of vectors in any basis of V. The dimension of a vector space V is notated as Dim(V). To understand it, think about ℝⁿ with basis,

the basis of ℝⁿ in this case is the easiest base of ℝⁿ. Then we can have the dimension of the vector space ℝⁿ as,
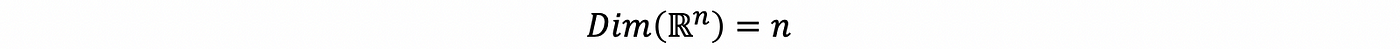
Suppose that if we have two bases of a vector space V, and the number of the vectors in these two bases are not equal. Could that happen? The answer is NO! The number of the vectors on any basis of a given vector space must be equal and be equal to rank (we will talk about it later). So there must be some redundancy problem or as we say independence issue in one of these two bases. Therefore, the definition is well-defined with any two bases have the same number of vectors in them.
(3) Basis: An example
Find a basis for N(A) when
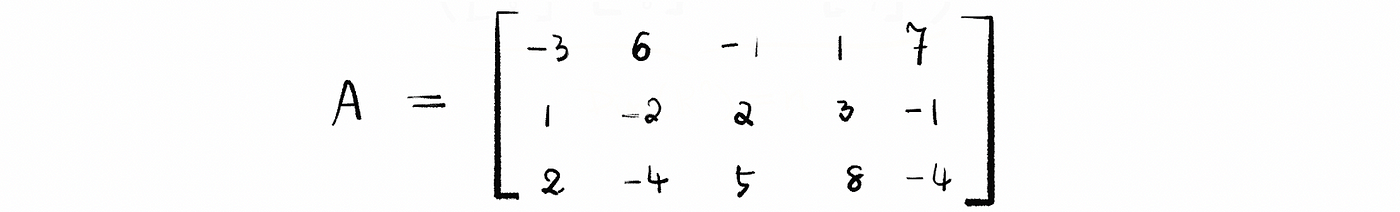
Ans:
Solve the equation Ax = 0 by row reduction to REF. So we have RREF as,
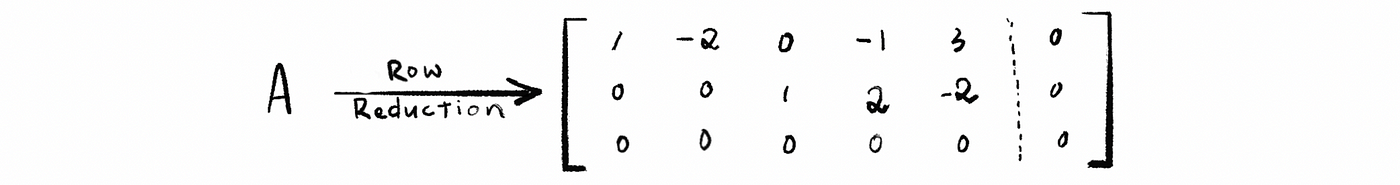
Note that we have 2 pivots in columns 1 and column 3, and we also have 3 free variables correspond to columns 2, 4, and 5.
Now we are going to choose x2 = 1, x4 = x5 = 0; x4 = 1, x2 = x5 = 0; x5 = 1, x2 = x4 = 0. So that means we just run into each of the free variables and set the value as 1 and then set the values of other free variables as 0.
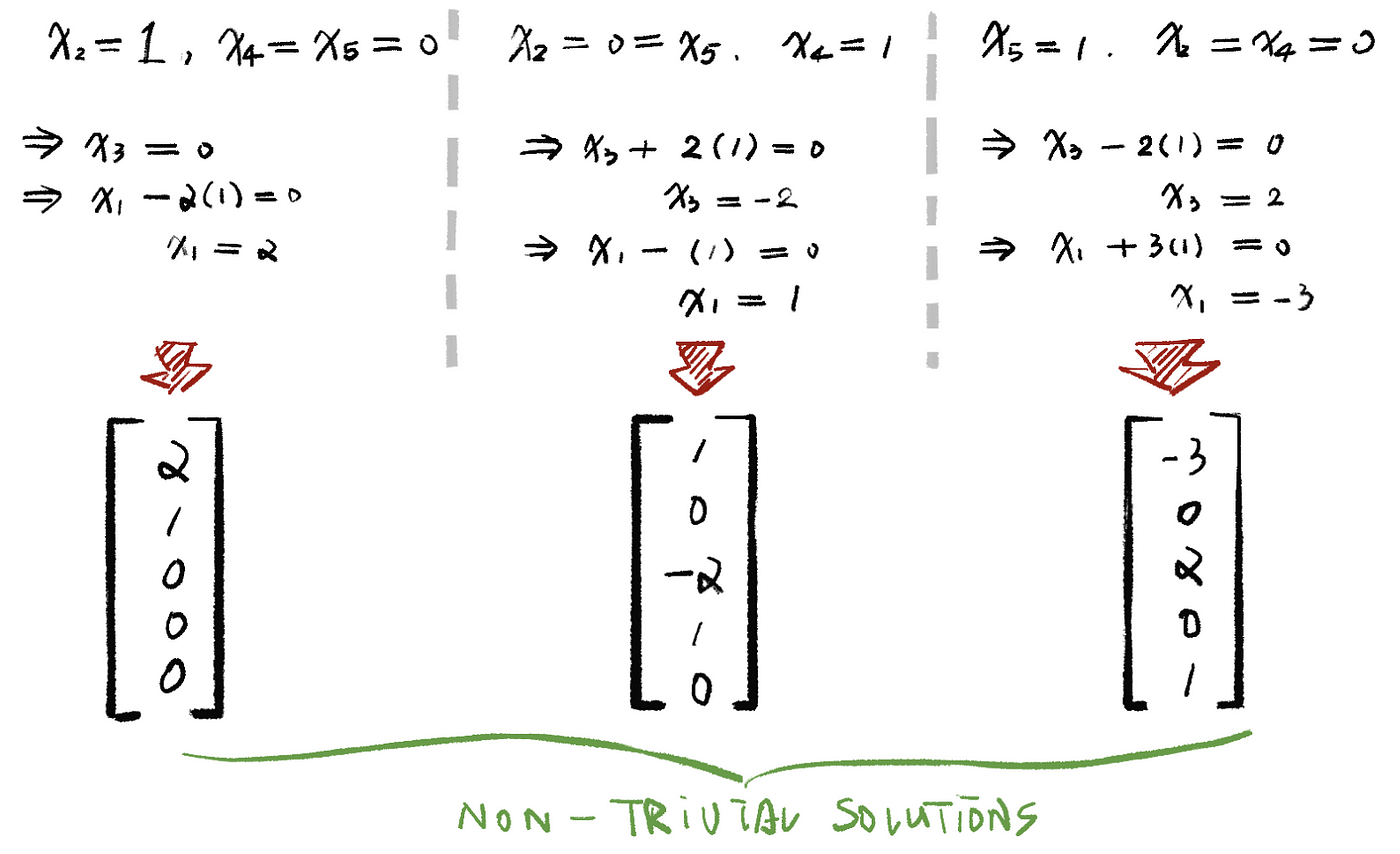
So we can calculate the null space of A, N(A), as,

and this set of vectors is a basis.
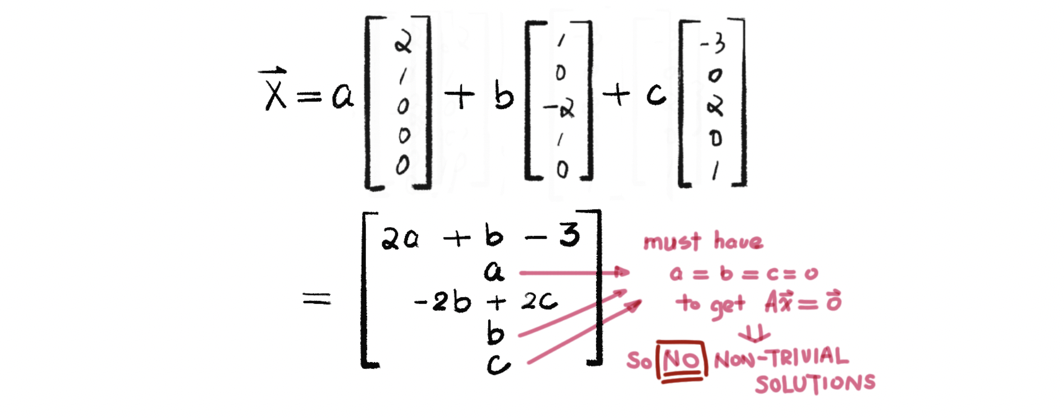
It is obvious that these vectors compose a spanning set for V. But why this set is linear independent? This is because the only way a linear combination of these can be zero is for all coefficients to be zero. For example, in the case above, suppose we have a, b, c ∈ℝ, so that,
(4) The Dimension of Null Space
In the previous case, we have already found the basis for N(A). Therefore, by the definition of dimension, the dimension of the null space N(A) equals the number of free variables in REF(A), (We have proved that all the non-trivial solutions are independent above.) which is also to say that,
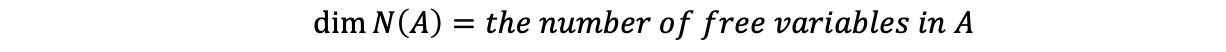
(5) Null Space in Geometry
Recall the definition of the null space as the span of all the non-trivial solutions to the homogenous system Ax = 0 and it is a subspace of ℝⁿ.
Because it is a subspace, it must have the property that this vector space goes through the origin, which is also,

Because the non-trivial solution is a vector from the origin to a point in the null space, then based on the fact that both of the starting point (origin) and the ending point is in this null space, we can derive that the vector is in this null space.
Also, based on the homogenous system Ax = 0 , we have,
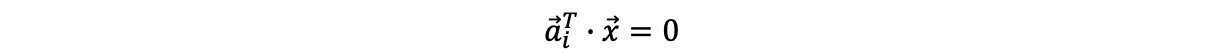
By the law of cosine, then
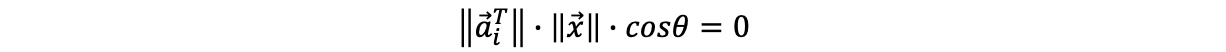
because x is a non-trivial solution,
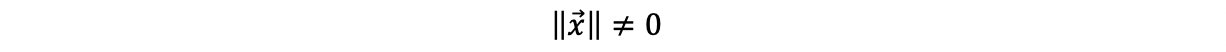
so, it is either,
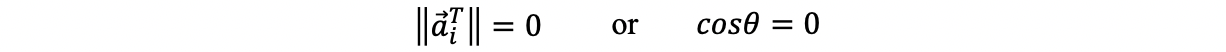
then, we have,
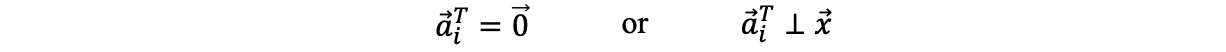
Now let's consider the easiest three examples in ℝ³,
- Suppose we have,
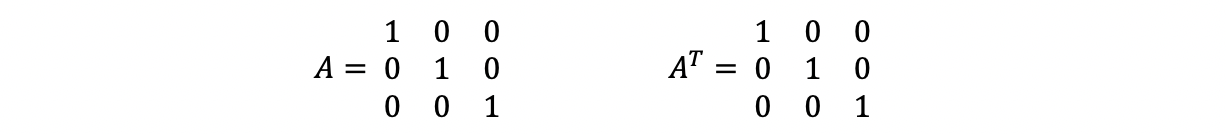
then, the column space of A transpose should be ℝ³ and the null space of A does not exist (because A has an only trivial solution to Ax = 0 ). We can also consider this by that we can never find a vector v in ℝ³ that is perpendicular to three orthogonal vectors (or as we say, perpendicular to the whole ℝ³ space).
- Suppose we have,
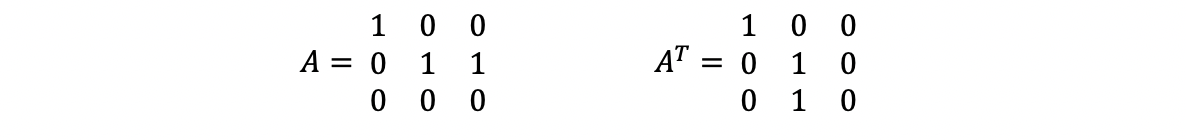
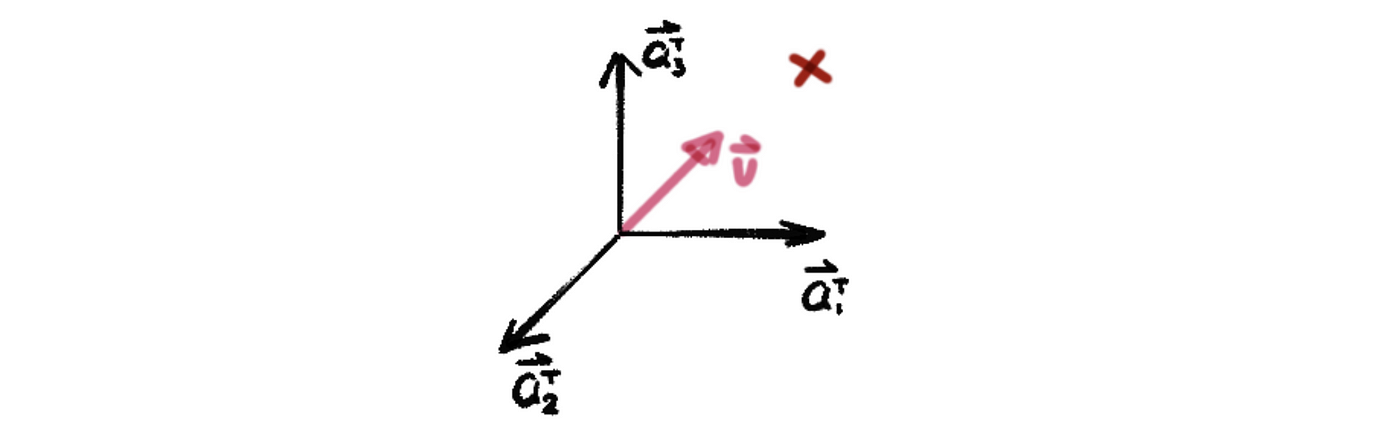
then, the number of pivots of A equals 2, and the number of free variables of A equals 1. Then the column space of A transpose can then be considered as span{[1 0 0], [0 1 1]}, and geometrically,
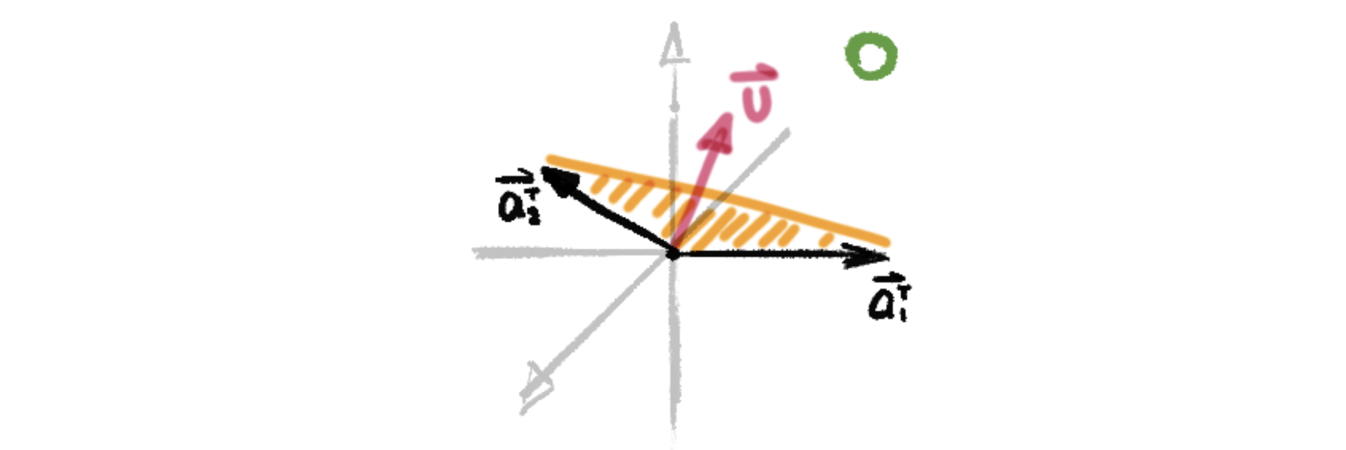
In this particular case, we can find a vector v in ℝ³ that is perpendicular to the two orthogonal vectors (or as we say, the plane that their linear combination represents). Thus, it is clear to see that our null space is a line that perpendicular to the column space of A transpose.
- Suppose we have,
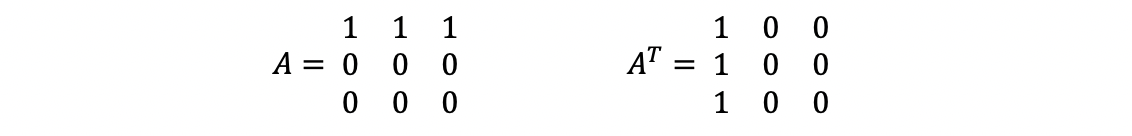
then, the number of pivots of A equals 1, and the number of free variables of A equals 2. Then the column space of A transpose can then be considered as span{[1 1 1]}, and geometrically (maybe ugly but I tried my best),
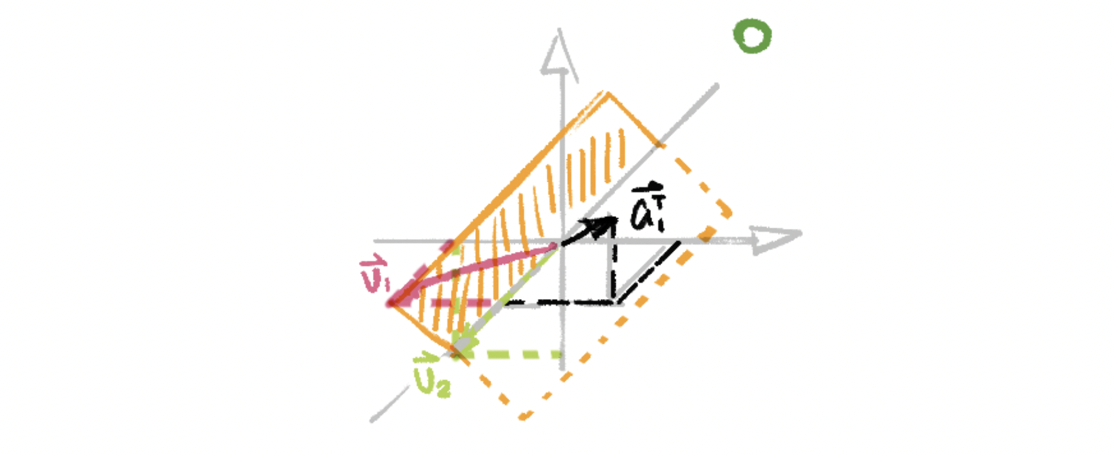
In this particular case, we can find two non-collinear vectors v 1, v 2 in ℝ³ that is perpendicular to the orthogonal vector (or as we say, the line that its linear combination represents). Thus, it is clear to see that our null space is a plane that perpendicular to the column space of A transpose.
In general, we can found out a solution that the name of the nullspace is because it is the non-trivial solutions that if transformed by matrix A, will be projected to a null vector. While however, under the view of geometry, the nullspace is the space that perpendicular to the column space of A transpose in the vector space. This is also,
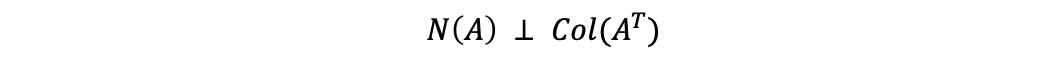
(5) The Dimension of Column Space
So what about Col(A)? How can we find a basis that is for Col(A)? Think about Ax = b , then

Recall the definition of the column space that W is a subspace of ℝᵐ and W equals the span of all the columns in matrix A. By doing row reduction, we can transfer A to its row echelon form. Based on its REF, we can draw the conclusion that some of the columns in A (free variables, if exist) could be represented by the linear combination of the other columns (pivot columns).
Thus, by definition of the basis of a subspace, the basis is the smallest (minimized) possible spanning set (without redundancy) or the largest (maximized) possible linearly independent set (because spanning) in the vector space V. So in this case, we can find the basis by finding the smallest possible spanning set, which is equivalent to the spanning set of all pivot columns. For example,
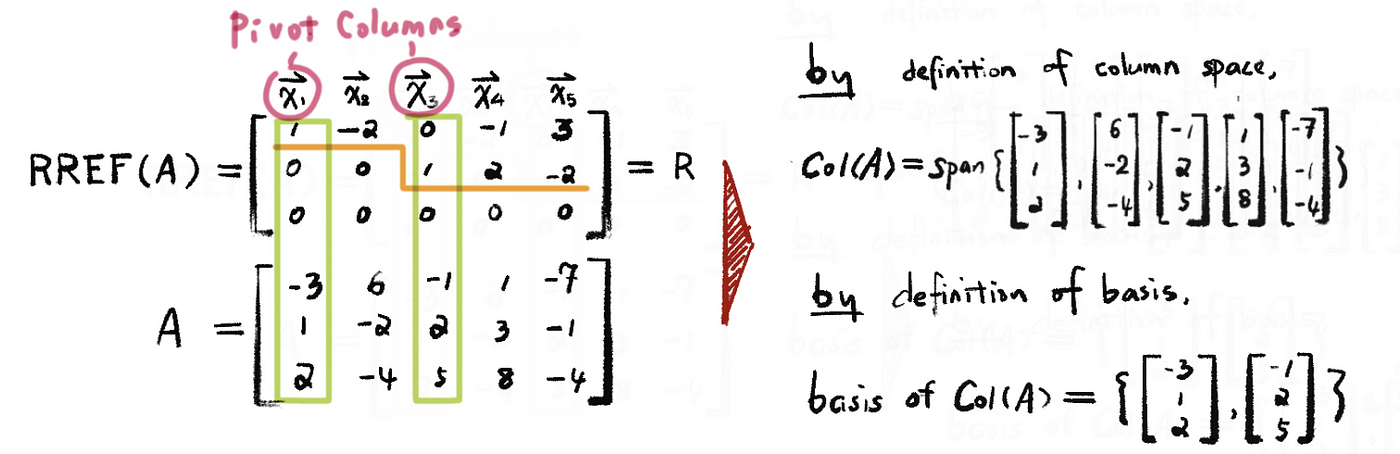
With the REF, we can find out that the non-pivot columns are linear combinations of the columns that proceed them.
If Ax = b has a solution, we can use pivot columns only to get b and the solutions are preserved but the vectors are not. So the basis for Col(A) is the columns of A corresponding to pivot columns in REF(A). And thus, the dimension of Col(A) equals the number of the pivot columns in REF(A). This is,
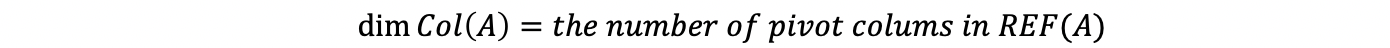
4. Rank and Row Space
(1) The Definition of Rank
Given a matrix A of m × n, and then the rank of A (notated as rank(A) or r) is the number of pivots in REF(A). So note that the rank of A rank(A) equals the dimension of Col(A).
If the size of A is m × n and if rank(A) = the number of pivots in A = r, then the number of non-pivot columns is,
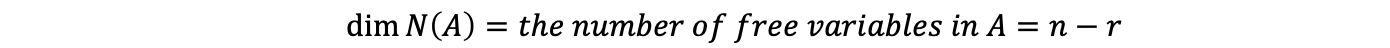
(2) Rank Nullity Theorem
Based on the previous proof, we have that,
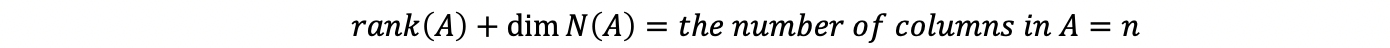
This is called the Rank Nullity Theorem. We can also have the following explanation as,
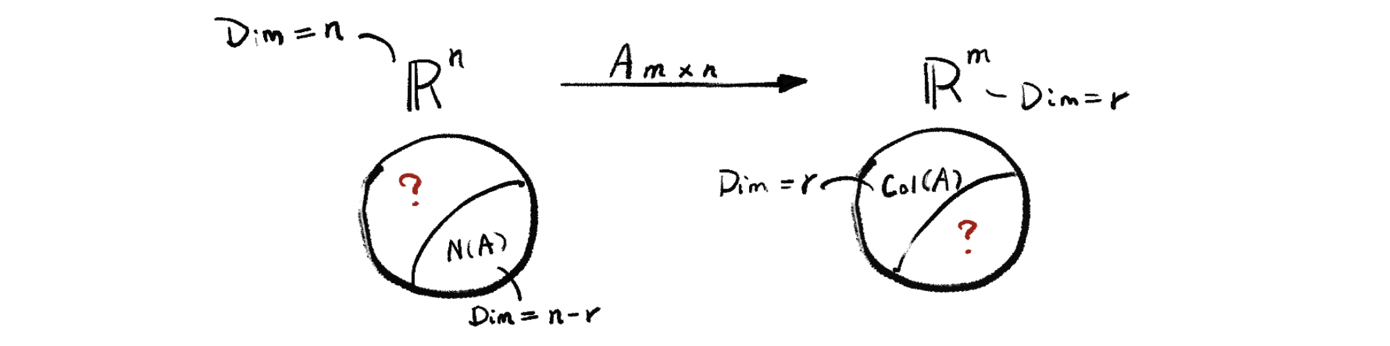
Because A can be reckoned as a transformation A: ℝⁿ → ℝᵐ, then, because the vectors in the basis of nullspace N(A) are all ∈ ℝⁿ, we then write N(A) in the left-hand side circle with its dimension Dim N(A) = n-r.
It is also quite clear that all the column vectors in A are in ℝᵐ space, so we write it in the right-hand side circle with its dimension Dim Col(A) = r.
So now our question is, can we find a subspace with all its vectors ∈ ℝⁿ, and its dimension equals r (the question mark on the left-hand side)? And can we find a subspace with all its vectors ∈ ℝᵐ, and its dimension equals m-r (the question mark on the right-hand side)?
You can think about it now and we will give the answer later in our following discussion.
(3) The Definition of Row Space
The row space of A of m × n equals the span of all rows in A (which is quite similar to the definition of the column space). (Row of A lives in the row space ℝⁿ). Therefore,

(4) The Dimension of a Row Space
It can be proved that any non-zero rows in RREF(A) are linearly independent (a conclusion after row reduction, and we are not going to prove it here), so the dimension of row space equals to the number of row vectors in its basis.
Therefore, the dimension of the row space of row A equals the number of non-zero rows in RREF(A). It also equals the number of pivots or the rank of A, rank(A), or the dimension of the column space Col(A).
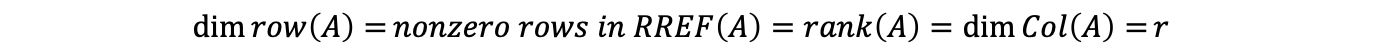
Because the row vectors in A ∈ ℝⁿ and the dimension of row space equals r, then we can solve the left-hand side part of the graph above as,
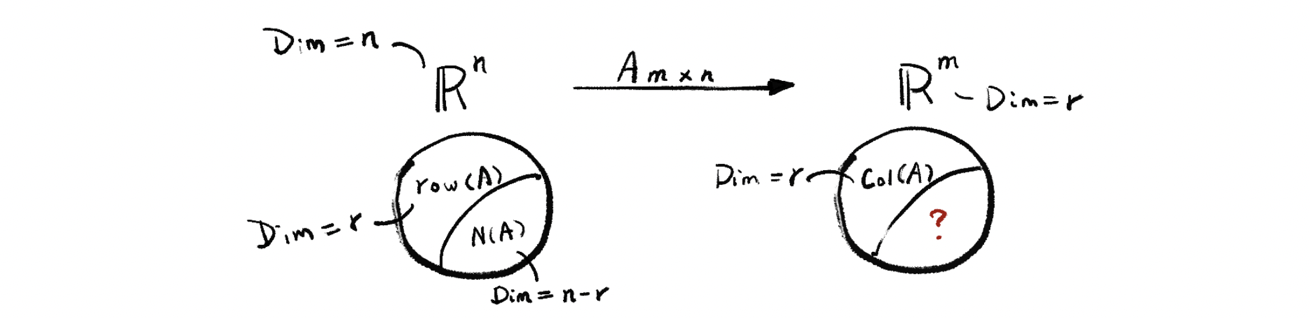
But we still have one question mark remains to be solved and we are going to discuss this in the next part.
Find a Basis of the Space of Solutions
Source: https://medium.com/adamedelwiess/linear-algebra-4-subspace-nullspace-column-space-row-space-basis-dimension-and-rank-9e03c625d913